Парная и множественная корреляция

(млн.руб.).

Для построения интервального прогноза рассчитаем доверительный интервал. Примем значение уровня значимости =0,05; следовательно, доверительная вероятность равна 95%, а критерий Стьюдента при равен 2,57.

Ширину доверительного интервала вычислим по формуле:

.

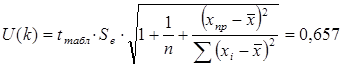Интервальный прогноз найдем по следующей формуле:

.

Верхняя граница равна: 14,472 (млн. руб.)

Нижняя граница: 13,157 (млн. руб.).

Фактические, расчетные и прогнозные значения по лучшей модели отобразим на графике (рис. 1.5).

. Результаты расчетов отобразим на графике.

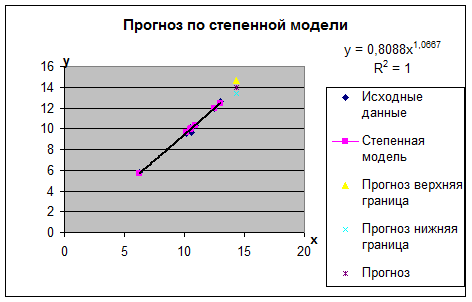
Рисунок 1.1. - Прогноз по лучшей (степенной) модели: х - объем капиталовложений, млн. руб.; y - объем выпуска продукции, млн. руб.

линейная регрессия корреляция прогнозный

2. Практическая задача 2

.1 Условие и исходные данные

Условие задачи: По десяти кредитным учреждениям получены данные, характеризующие зависимость объема прибыли (Y) от среднегодовой ставки по кредитам (X1), ставки по депозитам (Х2) и размера внутрибанковских расходов (Х3) (табл. 2.1).

Таблица 2.1 - Исходные данные: X1 - среднегодовой ставки по кредитам; Х2 -ставка по депозитам; Х3 - размер внутрибанковских расходов; Y - объема прибыли

Требуется:

. Осуществить выбор факторных признаков для построения двухфакторной регрессионной модели.

. Рассчитать параметры модели.

. Для характеристики модели определить:

- линейный коэффициент множественной корреляции,

- коэффициент детерминации,

- средние коэффициенты эластичности,

- бета - , дельта - коэффициенты.

Дать их интерпретацию.

. Осуществить анализ остатков (график и оценка с использованием d-критерия Дарбина-Уотсона).

. Осуществить оценку надежности уравнения регрессии.

. Оценить с помощью t-критерия Стьюдента статистическую значимость коэффициентов уравнения множественной регрессии.

. Построить точечный и интервальный прогнозы результирующего показателя.

. Отразить результаты расчетов на графике.